As artificial intelligence (AI) and machine learning (ML) technologies continue to advance, it’s essential to understand the difference between generative and discriminative models. Both models play a vital role in the field of ML and AI and are used for various applications, such as image recognition, speech processing, and natural language processing.
What are Generative Models?
Generative models aim to model the joint distribution of the input features and the target variable. In other words, they try to understand how the input data is generated and then use that understanding to generate new data that is similar to the original data. In contrast, discriminative models aim to model the conditional distribution of the target variable given the input features. They focus solely on predicting the output value given the input data.
Generative models are often used in unsupervised learning problems, where the goal is to learn the underlying structure of the data without any labeled examples. They can also be used in supervised learning problems, where the goal is to predict the target variable given the input features. Examples of generative models include Gaussian Mixture Models (GMMs), Hidden Markov Models (HMMs), and Variational Autoencoders (VAEs).
What are Discriminative Models?
Discriminative models, on the other hand, are primarily used in supervised learning problems, where the goal is to predict the target variable given the input features. They are also used in semi-supervised learning problems, where only a small subset of the data is labeled. Examples of discriminative models include logistic regression, decision trees, and neural networks.
Differences between Generative and Discriminative models
One significant advantage of generative models is their ability to generate new data that is similar to the original data. For example, VAEs can be used to generate new images by sampling from the learned distribution of the input data. This ability can be useful in applications such as image synthesis, where the goal is to create new images that are similar to the original data.
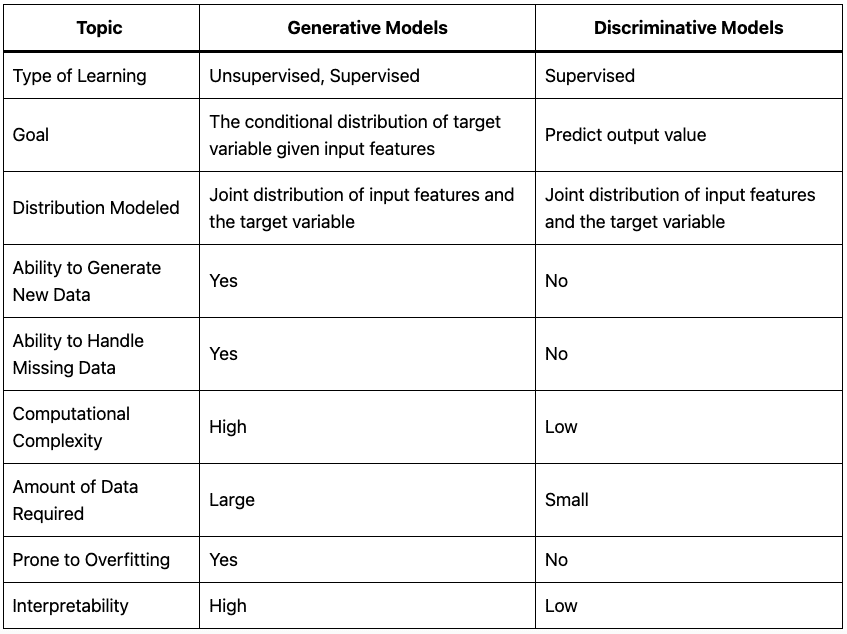
Another advantage of generative models is their ability to handle missing data. Since they model the joint distribution of the input features and the target variable, they can generate new data even if some of the input features are missing. This ability can be useful in applications such as data imputation, where missing data values need to be predicted.
However, generative models can be computationally expensive and challenging to train. They require large amounts of data to learn the underlying distribution of the input features and the target variable accurately. They are also prone to overfitting, where the model becomes too complex and performs poorly on new, unseen data.
Discriminative models, on the other hand, are generally easier to train and require fewer data than generative models. They focus solely on predicting the output value given the input data, which can be easier than modeling the entire joint distribution of the input features and the target variable. They are also less prone to overfitting than generative models since they have fewer parameters to learn.
However, discriminative models cannot generate new data, and they cannot handle missing data as well as generative models. They are also less interpretable than generative models since they do not model the entire joint distribution of the input features and the target variable.
Basic algorithm and mathematics behind generative and discriminative models
Now, let’s dive a bit deeper into the basic algorithm and mathematics behind generative and discriminative models.
Mathematics Behind Generative Models
Generative models aim to model the joint distribution of the input features and the target variable. In other words, they try to understand how the input data is generated and then use that understanding to generate new data that is similar to the original data.
One common algorithm for generative models is the Gaussian Mixture Model (GMM). GMMs assume that the data is generated by a mixture of Gaussian distributions. The algorithm then estimates the parameters of the Gaussian distributions (such as the mean and variance) that best fit the data.
Another popular generative model is the Variational Autoencoder (VAE). VAEs use a neural network to model the probability distribution of the input data. They then use this distribution to generate new data that is similar to the original data.
The basic mathematics behind generative models involves probability theory and statistics. For example, GMMs use the maximum likelihood estimation (MLE) method to estimate the parameters of the Gaussian distributions. MLE is a statistical method that estimates the parameters of a probability distribution that maximize the likelihood of the observed data.
VAEs use variational inference to approximate the posterior distribution of the input data. Variational inference is a method for approximating complex probability distributions by transforming them into simpler distributions that are easier to work with.
Mathematics Behind Discriminative Models
Discriminative models aim to model the conditional distribution of the target variable given the input features. They focus solely on predicting the output value given the input data.
One common algorithm for discriminative models is logistic regression. Logistic regression models the conditional probability of the target variable given the input features using a logistic function.
Another popular discriminative model is the neural network. Neural networks use a series of connected nodes to model the relationship between the input features and the target variable.
The basic mathematics behind discriminative models also involves probability theory and statistics. For example, logistic regression uses the maximum likelihood estimation (MLE) method to estimate the parameters of the logistic function. MLE is a statistical method that estimates the parameters of a probability distribution that maximize the likelihood of the observed data.
Neural networks use gradient descent to minimize a cost function that measures the difference between the predicted output and the actual output. Gradient descent is an optimization algorithm that iteratively adjusts the parameters of the model to minimize the cost function.
Recent trends and statistics
Recent statistics show that both generative and discriminative models have been used extensively in various applications. For example, generative models have been used in the field of computer vision to generate realistic images and synthesize new data. Discriminative models have been used in the field of natural language processing to perform sentiment analysis and text classification.
Recently, generative models are becoming increasingly popular. It is believed that the growing popularity of generative models is due to their potential to be used for a variety of tasks, including image generation, text generation, and data augmentation. The authors also believe that the growing popularity of generative models is due to the development of new techniques that make it easier to train these models.
Conclusion
In conclusion, generative and discriminative models use different algorithms and mathematical methods to achieve their respective goals. Understanding these algorithms and methods is essential for building and using effective ML and AI models. Generative models and discriminative models are two important types of machine learning models. Generative models are used to create new data, while discriminative models are used to classify data. The choice of whether to use a generative model or a discriminative model depends on the specific task at hand.


